|
|
|
|
Assistant Professor Faculty Office Building (FOB) S11 cohenm@newpaltz.edu Phone: 845-257-3525 |
Department of Mathematics, Faculty Office Building (FOB) E2 SUNY New Paltz, 1 Hawk Drive New Paltz, NY 12561-2443 Fax: 845-257-3571 |
Home
Teaching
Research
Conferences and Workshops
Tips for Young Mathematicians

Biking with Mathematicians
Moduli spaces of line arrangements (with undergraduates)
A complex projective line arrangement is a collection of complex projective lines in the complex projective plane, a 4-manifold. Given the combinatorial intersection data of these lines, the moduli space is the collection of all geometric realizations of this data. When this moduli space is a single connected component or two components that are complex conjugate to each other, the arrangement cannot be a Zariski pair (see below)

|
17. Classification of moduli spaces of 11-line arrangements with quadruples (joint with Jordan Buhmann, Alexander May, and Shiyu Shu) |
|

|
UNDERGRADUATE STUDENTS Jordan Buhmann '19, Alexander May '19, and Shiyu Shu '19: I worked with undergraduate math majors Jordan Buhmann, Alexander May, and Shiyu Shu (double major in economics) as part of Vassar's Undergraduate Research Summer Institute (URSI) the summer before their senior years. Alex is currently a graduate student at Queen's University in Canada. Shiyu is currently a graduate student at Carnegie Mellon University. |
|
|
16. On transformations of the complex projective plane and applications to line arrangements (joint with Jordan Buhmann, Baian Liu, Alexander May, and Shiyu Shu), preprint available |
||

|
UNDERGRADUATE STUDENT Sarah Goodhill, Vassar College '22: I worked with incoming first year student Sarah Goodhill as part of Vassar's Diving Into Research (DIR) the summer before she starts college at Vassar. She presented a poster on her project at the URSI symposium. Sarah showed that there exactly four simple arrangements of six real projective lines in RP^2 and that there are exactly eleven simple arrangments of seven real projective lines in RP^2, but this result had been proven already by several other people, including former Vassar professor Louise D. Cummings in the 1930s. |
|
|
UNDERGRADUATE STUDENT Kevin Ros, Vassar College '20: I worked with undergraduate computer science major Kevin Ros throughout his sophomore year and during the summer before his junior year. Kevin created a database for line arrangements. |
||
|
15. Moduli spaces of one-line extensions of (10_3)-configurations (joint with Baian Liu), preprint available |
||
|
UNDERGRADUATE STUDENT Baian Liu, Vassar College '18: I worked with undergraduate math major Baian Liu throughout his junior and senior years and as part of Vassar's Undergraduate Research Summer Institute (URSI) the summer before his senior year. Baian is currently a graduate student at The Ohio State University. |
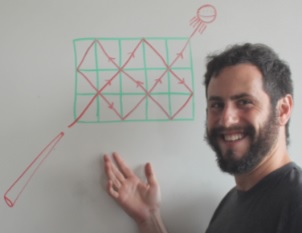
Random Chebyshev knots
Random knots go back several decades; in these models experimentalists distinguished small knots. The goal of a random knot diagram is to shed light on the relationship between knot invariants that can be computed directly from the diagram. Because of the nice combinatorial structure offered by the geometric parametrizations of knots by Chebyshev polynomials, these diagrams present a useful random knot model.
|
14. Crossing numbers of random two-bridge knots (joint with Chaim Even-Zohar and Sunder Ram Krishnan), Topology and its Applications 247 (2018) 100-114. http://arxiv.org/abs/1606.00277 | |
|
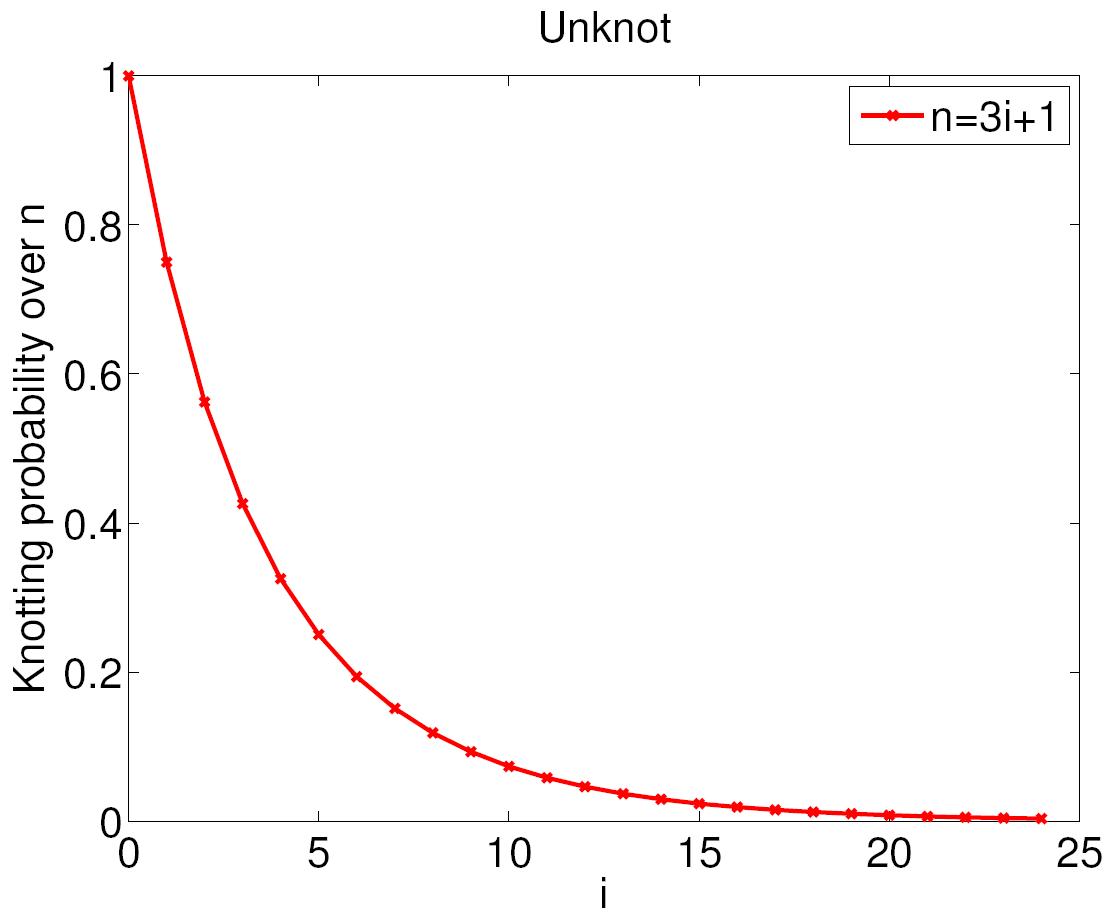
12. Random knots using Chebyshev billiard table diagrams, (joint with Sunder Ram Krishnan), Topology and its Applications 194 (2015) 4-21. http://arxiv.org/abs/1505.07681 |
|
| TALK 12. The probability of choosing the unknot among 2-bridge knots | ||
|
TALK 11. 6 reasons to love Chebyshev knots and billiard table diagrams | |
|
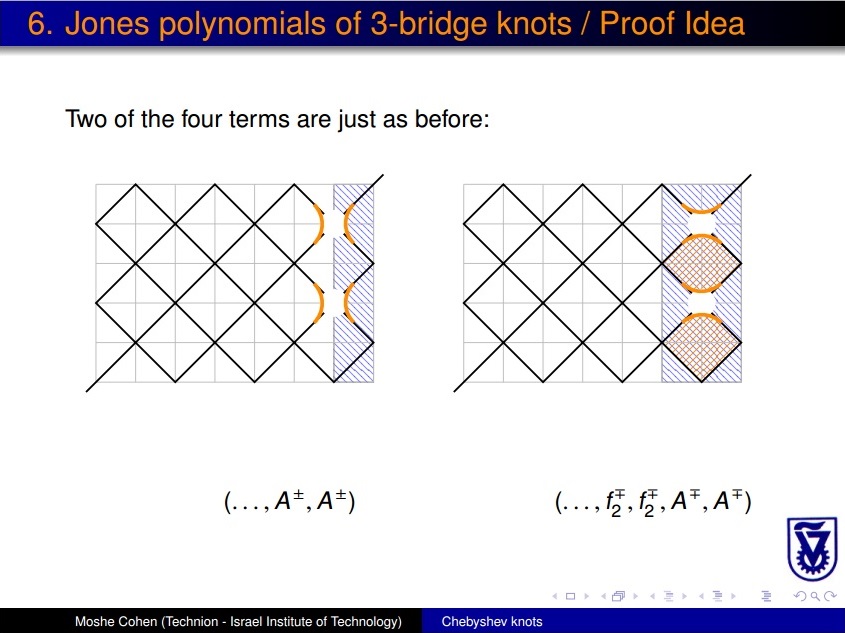
11. The Jones polynomials of 3-bridge knots via Chebyshev knots and billiard table diagrams, submitted, http://arxiv.org/abs/1409.6614, inspired by visits with and work of Pierre-Vincent Koseleff and Daniel Pecker of the University of Paris 6 |
||

|
EXPOSITORY ARTICLE. A Knot Game with _not KNerds, (joint with Allison Henrich), on games on knots, Math Horizons Vol. 20, Nov 2012. |
Zariski pairs of line arrangements
These are pairs of complex projective line arrangements with the same combinatorial intersection data but whose complements have different topological type. Surprisingly little is known about this class of objects, as very few examples exist. We search for candidates.

|
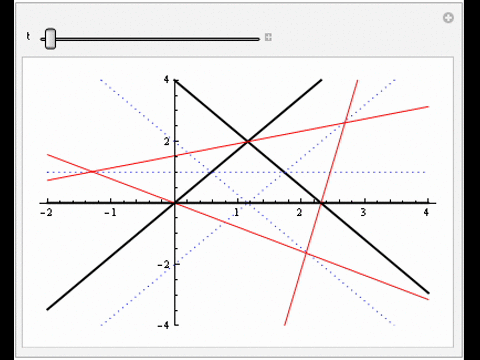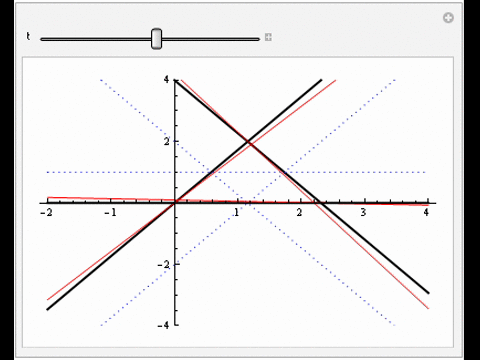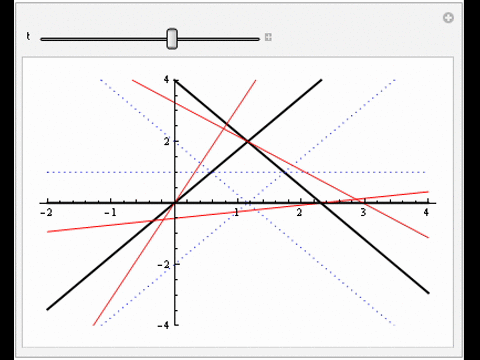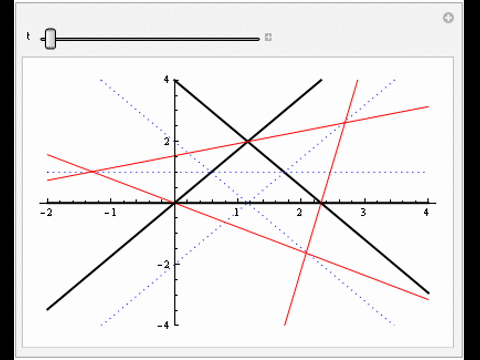
|
13. A distance between real line arrangements and examples (joint with Meirav Amram Topol, Hao Sun, and Mina Teicher), submitted |
| 9. Combinatorial symmetry of line arrangements and applications (joint with Meirav Amram Topol, Hao Sun, Mina Teicher, Fei Ye, and Anna Zarkh), Topology and its Applications 193 (2015) 226-247. http://arxiv.org/abs/1310.0700 | ||
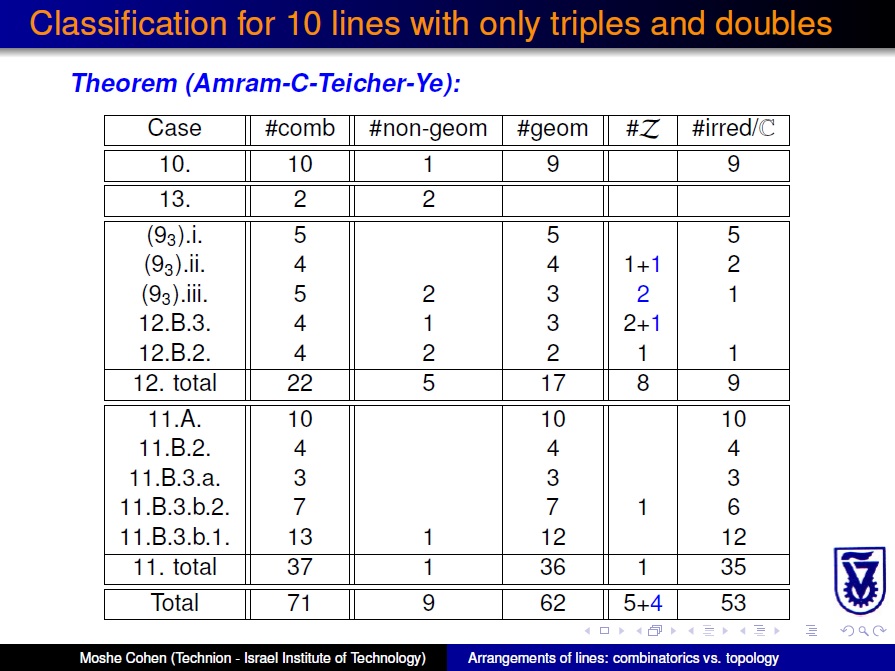
|
TALK 8-9. Arrangements of lines: when the combinatorics fails to understand the topology, mostly figures and tables to accompany a chalk talk | |
| 8. Moduli spaces of ten-line arrangements with double and triple points (joint with Meirav Amram Topol, Mina Teicher, and Fei Ye), submitted, http://arxiv.org/abs/1306.6105 | ||

|
VIDEOS 8. I created a pair of Geometry and Topology Today videos discussing my mathematics for a general audience and for graduate students together with Scott Baldridge and David Shea Vela Vick of the LSU Topology group. |
Dimer graphs from knots
Given a knot diagram, overlay both of its Tait checkerboard graphs on top of one another. This produces a plane bipartite graph with nice combinatorial structure.
Knots and dessin d'enfent
Knot diagrams as graphs on surfaces
|
10. The graded count of quasi-trees is not a knot invariant (previously called: A counterexample to Question 1 of ``A survey on the Turaev genus of knots'') (joint with Cody Armond),
Proceedings of the American Math. Society, Volume 144, (2016), no. 5, Pages 2285--2290,
http://arxiv.org/abs/1407.3259, answering a question of Abhijit Champanerkar and Ilya Kofman |
|
|
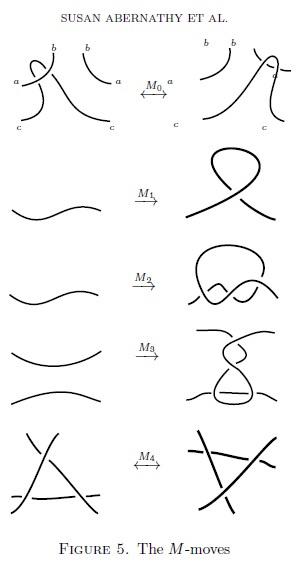
4. A reduced set of moves on one-vertex ribbon graphs coming from links (joint with Susan Abernathy, Cody Armond, Oliver Dasbach, Hannah Mannuel, Chris Penn, Heather M. Russell, Neal Stoltzfus), Proceedings of the American Math. Society 142 (2014), no. 3, 737-752. http://arxiv.org/abs/1112.5172 |
Knots and braid monodromy factorizations
| 5. Links arising from braid monodromy factorizations (joint with Meirav Topol Amram and Mina Teicher), Journal of Knot Theory and its Ramifications 23 (2014), no. 2, 1450009 (32 pages). http://arxiv.org/abs/1212.2193 | |

|
POSTER 5. Links arising from braid monodromy factorizations |
Counting lattice points in polytopes

|
1. The number of "magic" squares, cubes, and hypercubes (joint with Matthias Beck, Jessica Cuomo, and Paul Gribelyuk), American Mathematical Monthly 110 (2003), no. 8, 707-717. http://arxiv.org/abs/math/0201013 |
Submitted papers -- see the arXiv for a complete list:
| 13. | A distance between real line arrangements and examples, (joint with Meirav Amram Topol, Hao Sun, and Mina Teicher) |
preprint available | 2016 | submitted | |
| 11. | The Jones polynomials of 3-bridge knots via Chebyshev knots and billiard table diagrams, inspired by visits with and work of Pierre-Vincent Koseleff and Daniel Pecker of the University of Paris 6 |
arXiv:1409.6614, | Talk | 2014 | submitted |
| 8. | Moduli spaces of ten-line arrangements with double and triple points, (joint with Meirav Amram Topol, Mina Teicher, and Fei Ye) |
arXiv:1306.6105, | Talk, Video |
2013 | submitted |
Publications -- also see Google Scholar or MathSciNet:
| 14. | Crossing numbers of random two-bridge knots, (joint with Chaim Even-Zohar and Sunder Ram Krishnan) |
arXiv:1606.00277, | 2018 | Topology and its Applications 247 (2018) 100-114. | |
| 10. | The graded count of quasi-trees is not a knot invariant, (previously called: A counterexample to Question 1 of ``A survey on the Turaev genus of knots''), (joint with Cody Armond), answering a question of Abhijit Champanerkar and Ilya Kofman |
journal version, arXiv:1407.3259, MathSciNet |
2016 | Proceedings of the American Math. Society, Volume 144, (2016), no. 5, Pages 2285--2290, | |
| 12. | Random knots using Chebyshev billiard table diagrams, (joint with Sunder Ram Krishnan) |
arXiv:1505.07681, MathSciNet |
Talk | 2015 | Topology and its Applications 194 (2015) 4-21. |
| 9. | Combinatorial symmetry of line arrangements and applications, (joint with Meirav Amram Topol, Hao Sun, Mina Teicher, Fei Ye, and Anna Zarkh) |
arXiv:1310.0700, MathSciNet |
Talk, Video |
Topology and its Applications 193 (2015) 226-247. | |
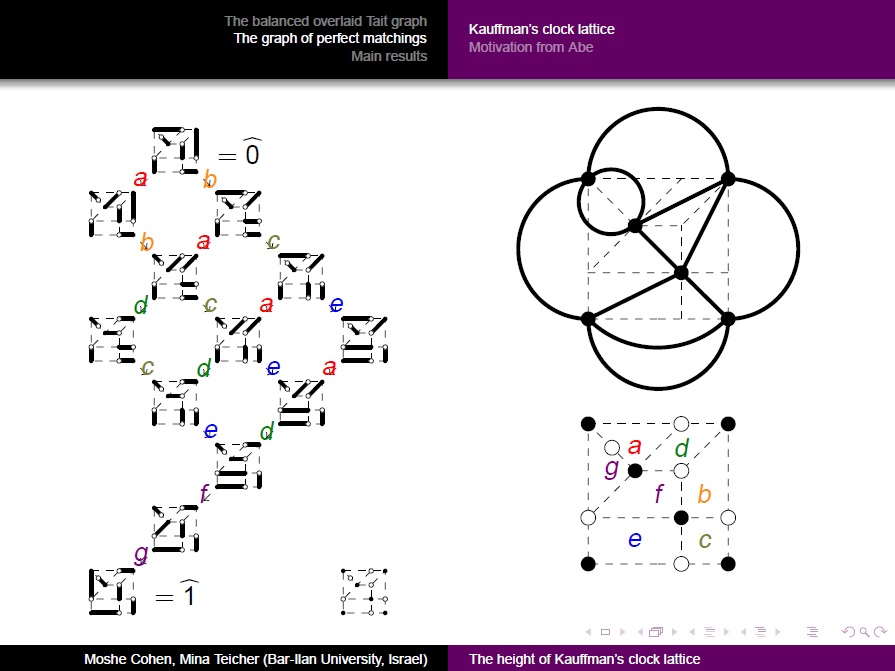
| 6. | Kauffman's clock lattice as a graph of perfect matchings: a formula for its height, (joint with Mina Teicher) |
journal version, MathSciNet |
Talk, Poster |
2014 | Electronic Journal of Combinatorics 21 (2014), no. 4, #P4.31. |
| 5. | Links arising from braid monodromy factorizations, (joint with Meirav Topol Amram and Mina Teicher) |
arXiv:1212.2193, MathSciNet |
Poster | Journal of Knot Theory and its Ramifications 23 (2014), no. 2, 1450009 (32 pages). | |
| 4. | A reduced set of moves on one-vertex ribbon graphs coming from links, (joint with Susan Abernathy, Cody Armond, Oliver Dasbach, Hannah Mannuel, Chris Penn, Heather M. Russell, Neal Stoltzfus) |
arXiv:1112.5172, MathSciNet |
Proceedings of the American Math. Society 142 (2014), no. 3, 737-752. | ||
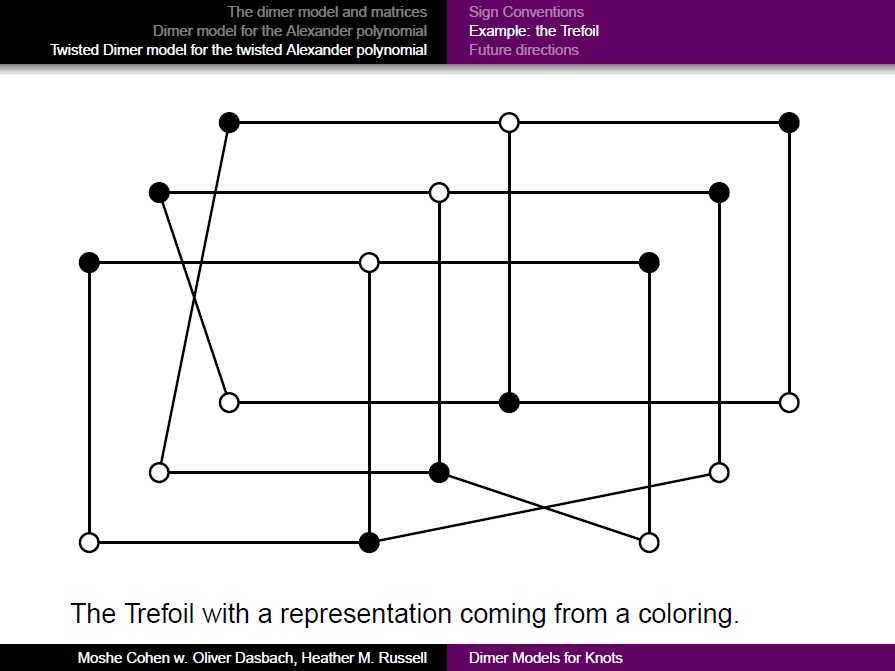
| 3. | A twisted dimer model for knots, (joint with Oliver Dasbach and Heather M. Russell) |
arXiv:1010.5228, MathSciNet |
Talk | Fundamenta Mathematicae 225 (2014), 57-74. | |
| 2. | A determinant formula for the Jones polynomial of pretzel knots | arXiv:1011.3661, MathSciNet |
Talk | 2012 | Journal of Knot Theory and its Ramifications vol. 21 (2012), no. 6, 1250062 (23 pages). |
| 1. | The number of "magic" squares, cubes, and hypercubes, (joint with Matthias Beck, Jessica Cuomo, and Paul Gribelyuk) |
arXiv:0201013, MathSciNet |
2003 | American Mathematical Monthly 110 (2003), no. 8, 707-717. |
Notes
| 7. | A correspondence between complexes and knots, a note to be included in the forthcoming book on Discrete Morse Theory by Bruno Benedetti and Alexander Engstrom |
arXiv:1211.2553 | 2012 | submitted |
Selected talks:
- 12. The probability of choosing the unknot among 2-bridge knots
- 11. 6 reasons to love Chebyshev knots and billiard table diagrams
- 8-9. Arrangements of lines: when the combinatorics fails to understand the topology, mostly figures and tables to accompany a chalk talk
- 6-7. Poster: Discrete Morse functions obtained from knots, made using the LaTeX package tikzposter
- 6. Kauffman's clock lattice as a graph of perfect matchings: a formula for its height
- 5. Poster: Links arising from braid monodromy factorizations
- 3. Dimer models for the Alexander and twisted Alexander polynomials of knots
- 2. A dimer model for the Jones polynomial of pretzel knots
Videos:
- Introducing the central problem in line arrangements for a general audience,
as part of Geometry and Topology Today with Scott Baldridge and David Shea Vela Vick of the LSU Topology group. - On the search for Zariski pairs of line arrangements among arrangements of ten lines for graduate students,
as part of Geometry and Topology Today with Scott Baldridge and David Shea Vela Vick of the LSU Topology group. - Lissajous-toric knots by Marc Soret and Marina Ville
- The tail of a quantum spin network by Mustafa Hajij, my math younger brother